Transformations for GCSE Maths - ppt download

$ 28.00

4.8 (464) In stock

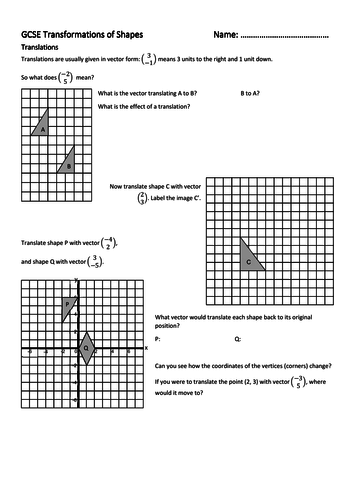
Translation Translations are usually given in vector form: means 3 units to the right and 1 unit down. So what does mean? What is the vector translating A to B? What about B to A? +3 A A to B: B to A: -3 B After translation, a shape will be the same shape and size the same way round (orientation) in a different position Back to main menu Next
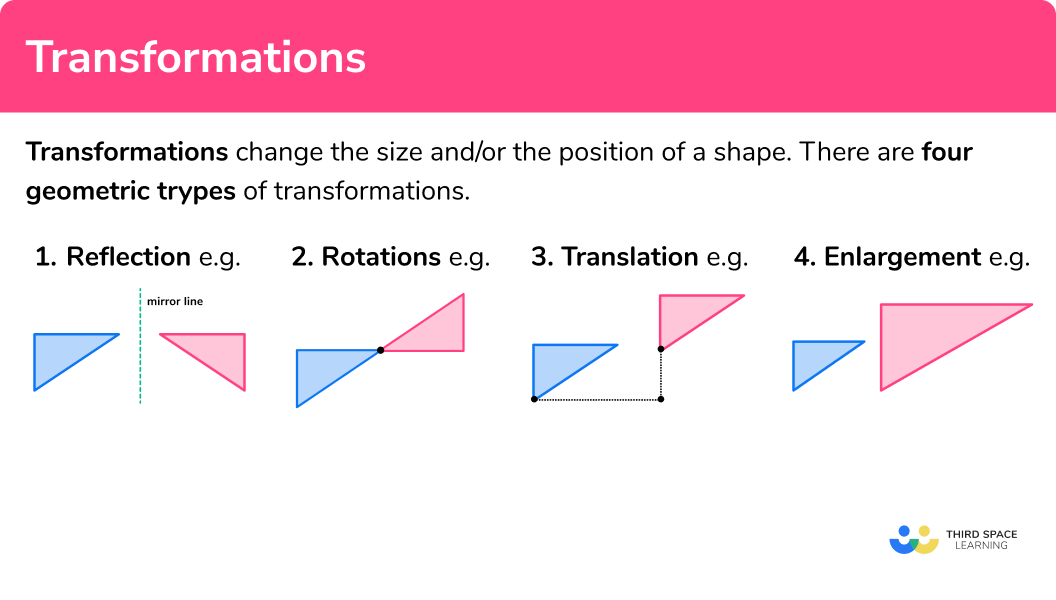
Rotation. Translation. Reflection. Invariant points. Enlargement. (Higher only)
means 3 units to the right. and 1 unit down. So what does mean What is the vector translating A to B What about B to A +3. A A to B: B to A: -3. B. After translation, a shape will be. the same shape and size. the same way round (orientation) in a different position. Back to main menu. Next.
Draw in the translation vector and mark the position of the corresponding corner on the translated shape. Repeat with the other corners until you are able to complete the shape. New location. of top corner. C’ 3 up. 2 right. C. Start here. Now translate shape C. with vector. Try the question before you click to continue! Back to main menu. Next.
x P’ New location. of bottom corner. Now try a couple more! P. Start here. Translate shape P. with vector. 2 up. -4 right. = 4 left. +3. Q. -5. Try it before you click to continue! Now translate shape Q. with vector. Q’ Try it before you click to continue! Can you see how the coordinates of the vertices (corners) change Look at the coordinates of one vertex at a time. What vector would translate each shape back to its original position Back to main menu. On to Reflection.
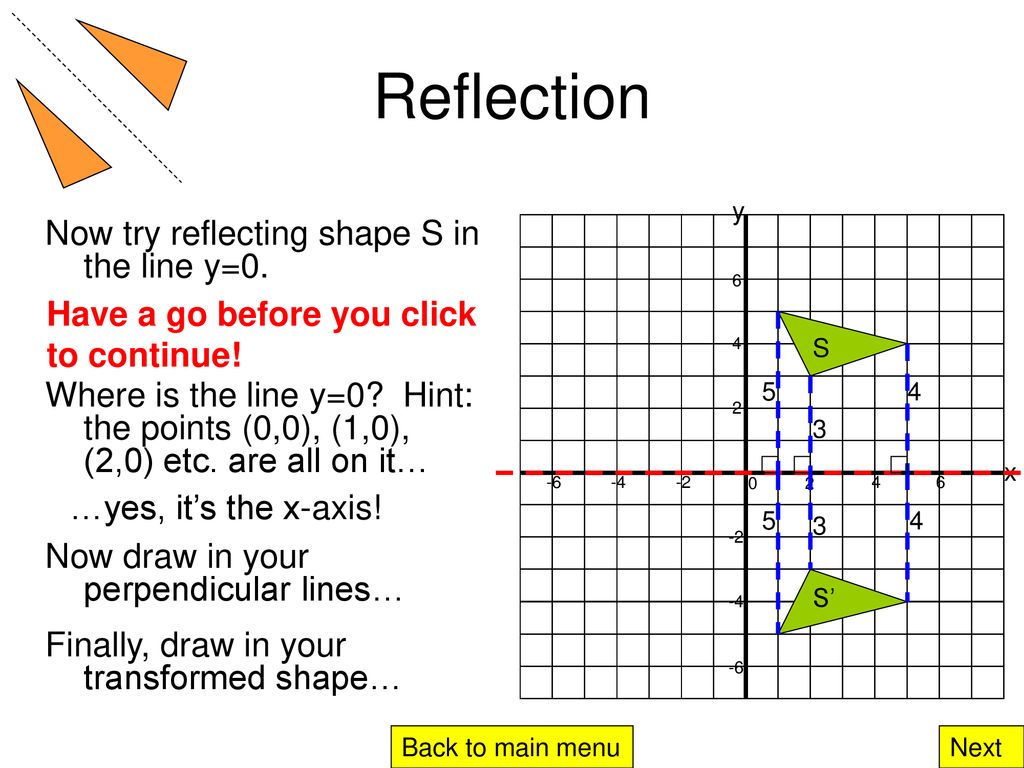
To draw the reflection, first draw the mirror line. Now draw a perpendicular line from one corner of the original shape to the mirror line, and extend it for the same distance on the other side (as on diagram above). Repeat with the other corners until you can draw the whole shape. Back to main menu. Next.
x Now try reflecting shape S in the line y=0. Have a go before you click to continue! 5. S. 4. Where is the line y=0 Hint: the points (0,0), (1,0), (2,0) etc. are all on it… …yes, it’s the x-axis! Now draw in your perpendicular lines… S’ Finally, draw in your transformed shape… Back to main menu. Next.
y. x Now reflect shape T in the line x=2… T T’ Try it before clicking to continue! … and then reflect shape T in the line y=x T’’ Try it before clicking to continue! Back to main menu. On to Rotation.
clockwise or anticlockwise. through 90, 180 or 270 degrees (quarter-, half- or ¾-turn) A piece of tracing paper can make this easier! Mark the centre of rotation and draw a straight line connecting it to one corner on the shape. Put tracing paper over both the shape AND the centre of rotation. Trace the shape and line onto the paper. Put your pencil point on the centre of rotation and turn the paper through the appropriate angle. Draw the transformed shape in its new position. Let’s give it a try… Back to main menu. Next.
First, mark your centre of rotation at (0,0) and join it to the shape. A. Place the tracing paper over the shape and the CoR, and trace. With your pencil point on the CoR, rotate the tracing paper clockwise through 90°, then transfer the shape to its new position on the grid. A’’ Now try rotating the same shape anticlockwise through 180° about the origin. A’ Try it, then click to see the answer. Back to main menu. Next.
Try it before clicking to continue! D. Can you think of another way to describe this transformation Click again for the answer… Rotation clockwise through 270° about the point (2, -1) D’ What transformation would return the shape to its original position Rotation clockwise through 90° (or anticlockwise through 270°) about the point (2, -1) Back to main menu. Next.
Try rotating shape F clockwise through 90° about the point (-1,2). F. F’ Have a go before clicking to see the answer! Back to main menu. On to Enlargement.
If the scale factor is more than 1, the shape will get bigger. e.g. a scale factor of 3 will result in a shape with sides 3 times as long (and 9 times the area!) If the scale factor is less than 1, the shape will get smaller – but it’s still called an enlargement! e.g. a scale factor of ½ will result in a shape with sides only half as long (and ¼ of the area!) For Higher you also have to be able to deal with negative scale factors – we’ll deal with these later on. Back to main menu. Next.
y. x Enlarge shape P about the origin with scale factor 2. P’ First, mark the centre of enlargement. 2→ and 8↑ Now draw a line from the CoE to one vertex (corner) on the shape. P. 1→ and 4↑ Multiply the length of line by the S.F. and extend it to find the position of the corresponding vertex on the enlarged shape. New. vertex. Extended line: 6→ and 2↑ Original line: 3→ and 1↑ Repeat with the other vertices until you have enough information to draw the new shape. Back to main menu. Next.
y. x Now enlarge shape Q about the point. (-4, -5) with scale factor ⅓. Q. Try it before clicking to see the answer! 6→ and 12↑ x ⅓ gives. 2→ and 4↑ Q’ 12→ and 3↑ x ⅓ gives. 4→ and 1↑ Back to main menu. Next.
y. x R’’ Now enlarge shape R about the point. (-2, 1) with scale factor 3. R’ Try it before clicking to continue! 1← and 2↑ x 3 gives. 3← and 6↑ Final question… R’’ is also an enlargement of shape R. Can you work out the scale factor and find the centre of enlargement R. Compare the side lengths: Scale factor = new length. old length. 3→ and 2↓ x 3 gives. 9→ and 6↓ So scale factor = 6/4 = 1.5. Now draw lines through the corresponding vertices of the two shapes, and extend them back until they meet; this point is the CoE. Centre of enlargement = (-5,-7) Back to main menu. Next.
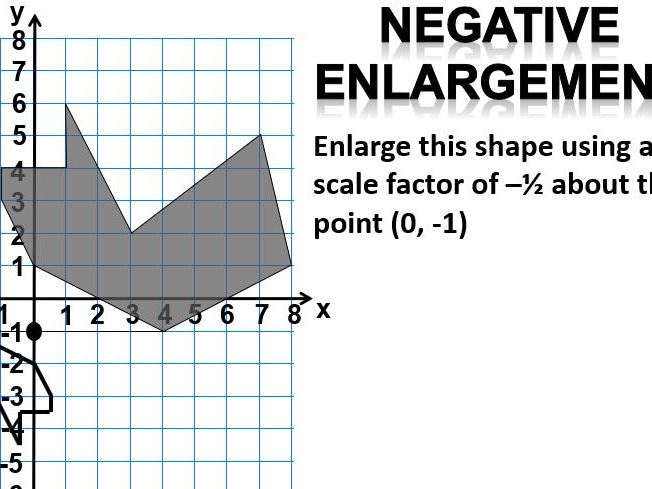
(Higher only) Enlargement (negative scale factor) y. x Enlarge shape S about the point (3, 1) with scale factor -2. First, mark the centre of enlargement. 1→ and 4↑ S. Now draw a line from the CoE to one vertex (corner) on the shape. Multiply the length of line by the S.F. and extend it in the opposite direction to find the position of the corresponding vertex on the enlarged shape. Image line: 6← and 2↓ Original line: 3→ and 1↑ New. vertex. S’ Repeat with the other vertices until you have enough information to draw the new shape. 2 ← and 8↓ Back to main menu. On to Invariant Points.
With a translation, every point moves by the same amount, so you’ll only have invariant points if the translation vector is … Answer: 0 0 , i.e. nothing moves, so every point on the shape is invariant. A’ A. A’’’ A’’ A’’’’ Back to main menu. Next.
Can you predict where there will be invariant points in the case of a reflection For example, try reflecting shape V in the line y = 3. There is just one invariant point; where is it Answer: (2, 3), i.e. the point that lies on the line of reflection. If one edge of a shape lies along the line of reflection then all points on that edge will be invariant. For example, let’s reflect shape W in the line y = 3. The set of invariant points is given by. {-6 ≤ x ≤ -3, y = 3}. y. x W. 4. V. 2. W’ 4. V’ 2. Back to main menu. Next.
With rotations, if the centre of rotation is on the shape then that point will be invariant. Looking at shape F, the centre of rotation is (-2, 1) so this point remains invariant while all the points around it rotate. What angle would you have to rotate through to have more than one invariant point Would the location of the centre of rotation matter Answer: Rotation through 360° (or any multiple of it) would result in the shape ending up back where it started, regardless of the centre of rotation, so all points on the shape would be invariant. y. x F. F’ Back to main menu. Next.
With enlargements, if the centre of enlargement is on the shape then that point will be invariant. When shape R is enlarged with scale factor 3 about (-3, 2)… … the centre of enlargement stays where it is and all the other points move outwards, so the only invariant point is (-3, 2). This is true regardless of whether the scale factor is greater or less than 1, positive or negative. What enlargement would give more than one invariant point Answer: An enlargement of SF. 1 about any point (resulting in all points on the shape being invariant). y. x R’ R. Back to main menu. End.